Introduction to Computational Thinking#
This chapter introduces the main concepts related to computational thinking by providing a summary of relevant topics in the areas of Linguistics and Computing in the past 200 years. The historic hero introduced in these notes is Noam Chomsky, considered one of the fathers of modern linguistics. His works have had an enormous impact on the Linguistics domain and the Theoretical Computer Science domain.
Note
The slides for this chapter are available within the book content.
Historic hero: Noam Chomsky#
Noam Chomsky (shown in Fig. 1) is one of the most prominent scholars of the last one hundred years. His contributions and research works have been disruptive and have changed the way scholars have approached several domains in science and humanities. He is described as one of the fathers of modern linguistics with Ferdinand de Saussure, Lucien Tesnière, Luis Hjelmslev, Zellig Harris, Charles Fillmore. In addition, he is one of the very first contributors and founders of the cognitive science field[1].
His approach to linguistics has been revolutionary, even if linguists have also debated it. The central aspect of his approach to human language is that mathematics can be used to represent the syntactic structure of a human language. Also, such a structure is biologically determined in all humans. It is already within us since birth, and it is a unique characteristic of human beings only and not of other animals. His view of human language is in high contrast with previous ideas about the evolution of languages, which intended a human being with no preconfigured linguistic structure. Thus, the language should have been a matter of learning a radically new endeavour from scratch.

Fig. 1 A picture of Chomsky taken in 2011. Photo by Andrew Rusk, source: Wikipedia.#
Among his extensive series of works in linguistics, the classification of formal grammars into a hierarchy of increasing expressiveness is undoubtedly one of his most important contributions, especially in the field of Theoretical Computer Science and Programming Languages. Formal grammar is a mathematical tool for defining a language, such as English. This tool permits the creation of a finite set of production rules that enable the construction of any valid syntactic sentence.
Each formal grammar is composed of a set of production rules in the form left-side ::= right-side (according to the Backus–Naur form, or BNF), where each side can contain one or more symbols of one or more of the following types:
terminal (specified between quotes in BNF), which identifies all the elementary symbols of the language in consideration (such as the nouns, verbs, etc., in English);
non-terminal (specified between angular brackets in BNF) identifies all the symbols in the formal grammar that can be replaced by a combination of terminal and non-terminal symbols.
Applying a production rule means that the sequence of symbols in the right-side part of the rule replaces those specified in the left-side part. The rewrite process done by the application of such production rules starts from an initial non-terminal symbol. In particular, one applies the production rules until they get a sequence of terminal symbols only. For instance, the production rules <sentence> ::= <pronoun> "write", <pronoun> ::= "I" and <pronoun> ::= "you" allows one to create all the two-word sentences having either the first or the second person singular pronoun accompanied by the verb write (e.g. “I write”). In addition, each formal grammar must specify a start symbol that must be non-terminal.
The hierarchy proposed by Chomsky provides a way for formally describing the relations between different grammars in terms of the possible syntactic structures that such grammars can generate. In practice, they are characterised by symbols in the left-side and right-side parts of production rules. These grammars are listed as follows, from the less expressive to the most expressive – we use letters from the Greek alphabet for indicating any possible combination of terminal and non-terminal symbols, including the empty characters (usually represented by ε):
regular grammars – form of production rules:
<non-terminal> ::= "terminal"and<non-terminal> ::= "terminal" <non-terminal>, as shwon in Listing 1.<sentence> ::= "I" <verb> <sentence> ::= "you" <verb> <verb> ::= "write" <verb> ::= "read"
context-free grammars – form of production rules:
<non-terminal> ::= γ, as shwon in Listing 2.<sentence> ::= <nounphrase> <verbphrase> <nounphrase> ::= <pronoun> <nounphrase> ::= <noun> <pronoun> ::= "I" <pronoun> ::= "you" <noun> ::= "book" <noun> ::= "letter" <verbphrase> ::= <verb> <verbphrase> ::= <verb> "a" <noun> <verb> ::= "write" <verb> ::= "read"
context-sensitive grammars – form of production rules:
α <non-terminal> β ::= α γ β, as shwon in Listing 3.<sentence> ::= <noun> <verbphrase> <sentence> ::= <subject pronoun> <verbphrase> "I" <verb> <object pronoun> ::= "I" "love" <object pronoun> "I" <verb> <noun> ::= "I" "read" "a" <noun> <verbphrase> ::= <verb> <noun> <verbphrase> ::= <verb> <object pronoun> <subject pronoun> ::= "I" <subject pronoun> ::= "you" <object pronoun> ::= "me" <object pronoun> ::= "you" <noun> ::= "book" <noun> ::= "letter"
recursively enumerable grammars – form of production rules:
α ::= β(no restriction applied), as shwon in Listing 4.<sentence> ::= <subject pronoun> <verbphrase> "I" <verb> <object pronoun> ::= "I" <verb> "you" "I" <verb> <noun> ::= "I" "read" "a" "book" <verbphrase> ::= <verb> <noun> <verbphrase> ::= <verb> <object pronoun> <subject pronoun> ::= "I" <subject pronoun> ::= "you" <object pronoun> ::= "me" <object pronoun> ::= "you" <verb> ::= "love" <verb> ::= "hate"
What is a computer?#
The English Oxford Living Dictionary defines the term computer as an “electronic device which is capable of receiving information (data) in a particular form and of performing a sequence of operations […] to produce a result”. However, the original definition of the same term, in use from the 17th century, is slightly different. It refers to someone “who computes” or a “person performing mathematical calculations” – from Wikipedia. In this chapter, when we use the term “computer”, we always consider the most generic definition: any information-processing agent (i.e. a machine or a person acting mechanically if appropriately instructed) [Nar19] that can make calculations and produce some output starting from input information.
Human computers, i.e. groups of people who have to undertake long calculations for specific experiments or measurements, have been used several times in the past. For instance, in Astronomy, human computers have been used for calculating astronomical coordinates of non-terrestrial things – such as the calculation of passages of Halley’s Comet by Alexis Claude Clairaut and colleagues. Napoleon Bonaparte used human computers, as well. He imposed the creation of mathematical tables to convert from the old imperial system of measurements to the new metric system [CK09, Roe10].

Fig. 2 Babbage Difference Engine No. 2 built at the Science Museum (London) and displayed at the Computer History Museum in Mountain View (California). Picture by Allan J. Cronin, source: Wikimedia Commons.#
In 1822, Charles Babbage, understanding the complexity of doing all these calculations by hand without introducing any error, started the development of an incredible machine. This machine was called the Difference Engine, a mechanical calculator, shown in Fig. 2. It aimed at addressing similar tasks that were run by human computers but in a way that was automatic, faster, and error-free. Babbage was able to build just a partial prototype of this machine, and, after the first enthusiasm, he was struggled by the limited flexibility that it offered. The Difference Engine was not a programmable machine. It was able to compute only a fixed set of operations on the inputs specified physically by changing specific configurations of the machine.
In order to address these limitations, in 1837, Babbage started to devise a new machine, the Analytical Engine, summarised in Fig. 3. Unfortunately, Babbage built no prototypes of this machine. However, by using it, a user could create any possible procedural calculation, making it the very first mechanical general-purpose computer in history. Furthermore, in contrast to its predecessor, the Analytical Engine received the input instructions and data using punched cards. The use of such cards prevented the users from making any physical manipulation of the machine to get it working.
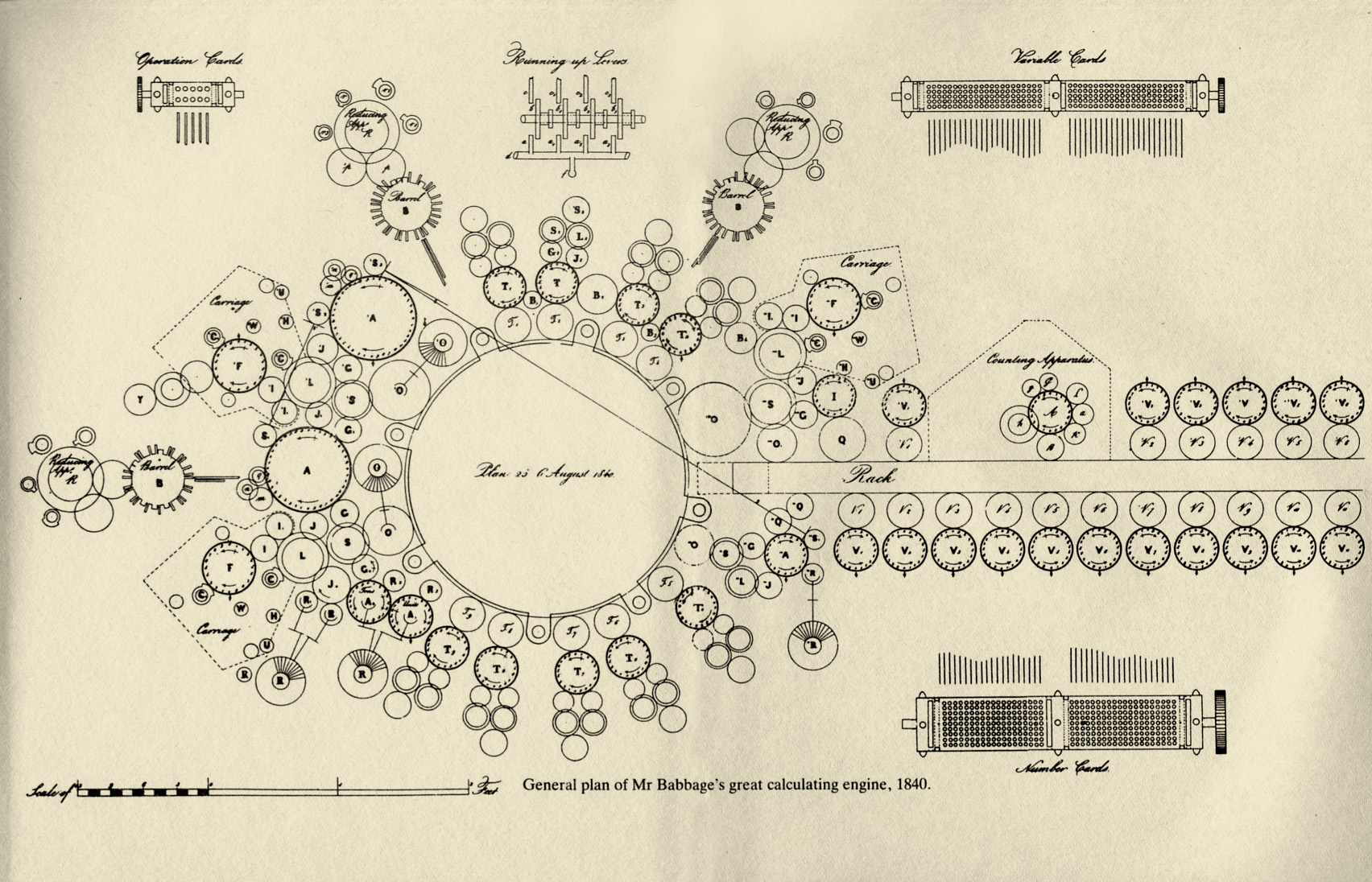
Fig. 3 A sketch by Babbage that describes the architecture of the Analytical Engine. Source: The Analytical Engine: 28 Plans and Counting, Computer History Museum.#
The ideas presented in the Analytical Engine were developed in a physical machine only one century later. Computing technology has had a drastic change as a consequence of World War II. Military research ordered the construction of several calculators. For instance, the Bombe (1940), designed by Alan Turing and based on previous works by Marian Rejewski and associates [Inm20], was the main instrument used by a group of people living in the secret British military camp at Bletchley Park to decipher German’s communications encrypted through the Enigma machine.
The Bombe was a handy and efficient machine. However, it was still partially based on mechanical components, and it allowed their users only a specific task. Nonetheless, it was crucial from a purely historical point of view. The first fully digital computer theoretically compliant with Babbage’s Analytical Engine was developed in the United States only a few years later, in 1946. It was the Electronic Numerical Integrator and Computer (ENIAC), shown in Fig. 4, that was programmable through patch cables and switches. This invention represents one of the most important milestones of the history of computers - the fixed point in time that generated all modern computers.

Fig. 4 A picture of the ENIAC in the Ballistic Research Laboratory (Maryland). Source: Wikipedia.#
Natural languages vs programming languages#
There is an aspect of computers (either humans or machines) that has not been tackled yet: which mechanism can we use to ask them to address a particular task? This aspect relates to the specific communication channel we want to adopt. For example, considering human computers, we can use the natural language (e.g. English) to instruct them in addressing specific actions.
A natural language is just an ordinary language (e.g. English), either written or oral, that has evolved naturally in humans, usually without specific and deliberate planning. As we know them, natural languages have the advantage (and, on the other hand, disadvantage) of being so expressive that particular instructions provided by using them can sound ambiguous. Consider, for instance, the sentence “shot an elephant in your pyjamas”. Does it mean one has to shoot an elephant (with a rifle) while wearing pyjamas? Or that one should shoot an elephant (with a water gun) drawn in pyjamas? We could develop specific (e.g. social) conventions that allow us to restrict the possible meaning of a situation. In the previous example, the fact that one is in a bedroom and is not living in Gabon is enough for disambiguating the sentence. While natural languages are not formal by definition, several studies in Linguistics try to provide their formalisation using some mathematical tool, e.g. [Ber02]. Even if one can formally define a natural language, its intrinsic vagueness is still present in the language itself. For instance, one cannot use mathematics (or, better, logic) for removing (all) the ambiguities from a natural language.
Programming languages, on the contrary, are formal-born languages. They oblige to specific syntactic rules. Such rules avoid possible ambiguous statements, mainly by restricting the expressiveness of the language. Therefore, all the sentences in such language are conveying just one possible meaning. Usually, they are based on context-free grammars, according to Chomsky’s classification introduced in Section Historic hero: Noam Chomsky. Also, they can have a significant degree of abstraction. In particular, we can distinguish three macro-sets of programming languages.
Machine language#
Machine language is a set of instructions that can be executed directly by the central processing unit (CPU) of an electronic computer. For instance, the binary executable code (i.e. a sequence of 0 and 1) defining a function (i.e. a kind of tool that takes some inputs and produces some output) for calculating the nth Fibonacci number is shown in Listing 5.
100010110101010000100100000010001000001111111010000000000111011100000110101110000000000000000000000000000000000011000011100000111111101000000010011101110000011010111000000000010000000000000000000000001100001101010011101110110000000100000000000000000000000010111001000000010000000000000000000000001000110100000100000110011000001111111010000000110111011000000111100010111101100110001001110000010100101011101011111100010101101111000011
Low-level programming languages#
Low-level programming languages are languages that provide one abstraction level on top of the machine language. Thus it allows one to write programs in a way that is more intelligible to humans. The most popular language of this type is Assembly. Even if it introduces humanly recognisable symbols, one line of assembly code typically represents one machine instruction in machine language. For instance, the same function for calculating the nth Fibonacci number is defined in Assembly in Listing 6.
1fib:
2 movl %edi, %eax
3 testl %edi, %edi
4 je .return_from_fib
5 cmpl $2, %edi
6 jbe .return_1_from_fib
7 movl %edi, %ecx
8 movl $1, %edx
9 movl $1, %esi
10.fib_loop:
11 leal (%rsi,%rdx), %eax
12 cmpl $2, %ecx
13 je .return_from_fib
14 movl %edx, %esi
15 decl %ecx
16 movl %eax, %edx
17 jmp .fib_loop
18.return_1_from_fib:
19 movl $1, %eax
20.return_from_fib:
21 ret
High-level programming languages#
High-level programming languages are characterised by a strong abstraction from the specifiability of the machine language. In particular, it may use natural language words for specific constructs to be easy to use and understand by humans. Generally speaking, the more abstraction from the low-level programming languages is provided, the more understandable the language is. For instance, in Listing 7, we show how to use the C programming language for implementing the same function as before.
1unsigned int fib(unsigned int n) {
2 if (n <= 0)
3 return 0;
4 else if (n <= 2)
5 return 1;
6 else {
7 unsigned int a,b,c;
8 a = 1;
9 b = 1;
10 while (1) {
11 c = a + b;
12 if (n <= 3) return c;
13 a = b;
14 b = c;
15 n--;
16 }
17 }
18}
Implementations in natural language#
We can also apply an additional level of abstraction to the previous example. For instance, we can provide natural language instructions to enable a human-computer to execute the function mentioned above. Of course, none of the macro-sets discussed above includes the natural language. However, the natural language would allow us to see how we can use an even more abstract language for instructing someone else to execute the same operation. In particular, a possible natural language description of the Fibonacci function could be:
The function for calculating the nth Fibonacci number takes as input an integer “n”. If “n” is less than or equal to 0, then 0 is returned as a result. Otherwise, if “n” is less than or equal to 2, then 1 is returned. Otherwise, in all the other cases, associate the value “1” to two distinct variables “a” and “b”. Then, repeat the following operations indefinitely until a value is returned. Set the variable “c” as the sum of “a” plus “b”. If “n” is less than or equal to “3” then return “c”, otherwise assign the value of “b” to “a” and the value of “c” to “b”, and finally decrease the value of “n” by 1 before repeating.
While the previous natural language definition maps perfectly the function defined in the machine binary code introduced above, other possible implementations of such Fibonacci function are possible. For example, one of the most famous that uses the concept of recursion could be:
The function for calculating the nth Fibonacci number takes as input an integer “n”. If “n” is less than or equal to 0, then 0 is returned as a result. Otherwise, if “n” is equal to 1, then 1 is returned. Otherwise, return the sum of the same function with “n-1” as input and still the same function with “n-2” as input.
Abstraction is the key#
We often say that we program a computer – where the word computer refers to an electronic computer. However, according to the definition we have provided in this document, computers can be both humans and machines. Thus, the verb to program is not very well suited when referring to human computers – we cannot program a person, can we? In this latter case, we usually say that we talk with a person to instruct her to execute specific actions through a (natural) language used as a communication channel. Thus, we think that, in this context, we should use the same verbs, i.e. to talk and to instruct, even when we refer to an electronic computer. Writing a program is precisely that: communicating to an electronic computer in a (formal) language that such an electronic computer and the human instructor can both understand [Pap80].
First, we need to agree on the language to use to communicate between us and a computer (either human or machine). Then, we can start to think about possible instructions that, if followed systematically, can return the expected result to a particular problem. To reach this goal, we (even unconsciously) try to figure out possible solutions to such a problem by comparing it with other possible recurring situations that happened in the past. The idea is to find some patterns that depict a viable solution for a set of abstractly homogeneous cases. Once found, the solution can be reused to reach our goal if it has been successful in the past. For instance, let us consider the actions that we perform at a post office. Some steps are similar to those we perform when we wait for our turn to play with a slide in the playground – as shown in Fig. 3.

Fig. 5 Two pictures that depict the same situation, i.e. queuing, in two different contexts: a playground (left) and a post office (right). Left photo by Prateek Rungta, source: Flickr. Right photo by Rain Rabbit, source: Flickr.#
Considering the situations and contexts mentioned above, we call computational thinking a particular approach to “solving problems, designing systems and understanding human behaviour that draws on concepts fundamental to computing” [Win08]. Thus, computational thinking is the thought process involved when we formulate a problem and express the solution by using a language that a computer (either human or machine) can understand and execute.
Jeannette Wing provides an additional definition for clarifying what computational thinking is about [Win08]:
Computational thinking is a kind of analytical thinking. It shares with mathematical thinking in the general ways in which we might approach solving a problem. It shares with engineering thinking in the general ways in which we might approach designing and evaluating a large, complex system that operates within the constraints of the real world. It shares with scientific thinking in the general ways in which we might approach understanding computability, intelligence, the mind and human behaviour.
It is important to stress that computational thinking is not a new subject at all. Instead, it focuses on specific aspects concerning computer science: the founding principles and methods instead of those merely related to particular tools and systems that people (often and erroneously) associate with any computer scientist, e.g. the electronic computer [Nar19].
The primary notion related to computational thinking is abstraction: the “process of leaving out of consideration one or more properties of a complex object […] by extracting common features from specific examples” [Kra07]. As highlighted in Fig. 5, the skill of abstracting situations and notions into symbols is crucial for automating task execution using a computer responsible for interpreting such abstractions. However, usually, we use these abstractions unconsciously. One of the goals of computational thinking is to reshape the abstractions we have ingested as a consequence of our life experiences – that we are often unconsciously reusing. Thus, being again fully conscious of such abstractions, we can use an appropriate language to make them understandable to a computer to automatise them.
The final goal of computational thinking is to teach the basic notions of computer science to all students, independently from their academic roots. Computational thinking should complement the other thinking strategies one has already learned in the past [Nar19]. And it applies either to academic research (including in the Humanities, e.g. see the use of computational models and techniques in History research [AYJ11, Mul18, PK15]) or in real-life tasks. No one is saying that this way of thinking is the right one, of course. However, it indeed offers a complementary tool to describe reality [Nar19]. In the future, computational thinking “will be an integral part of childhood education” [Win08]. It will affect how people think and learn and “the way other learning takes place” [Pap80].
References#
Ching-man Au Yeung and Adam Jatowt. Studying how the past is remembered: towards computational history through large scale text mining. In Proceedings of the 20th ACM international conference on Information and knowledge management, 1231–1240. Glasgow Scotland, UK, October 2011. ACM. URL: https://adammo12.github.io/adamjatowt/cikm11a.pdf (visited on 2024-08-31), doi:10.1145/2063576.2063755.
Raffaella Anna Bernardi. Reasoning with Polarity in Categorial Type Logic. PhD Thesis, Universiteit Utrecht, Utrecht, The Netherlands, 2002. URL: https://dspace.library.uu.nl/handle/1874/614.
Martin Campbell-Kelly. Origin of Computing. Scientific American, 301(3):62–69, September 2009. doi:10.1038/scientificamerican0909-62.
David Inman. Rejewski & Enigma. Patterns, 1(1):100011, April 2020. doi:10.1016/j.patter.2020.100011.
Jeff Kramer. Is abstraction the key to computing? Communications of the ACM, 50(4):36–42, April 2007. doi:10.1145/1232743.1232745.
Lincoln A. Mullen. Computational Historical Thinking: With Applications in R. Self-published, 2018. URL: https://dh-r.lincolnmullen.com/.
Enrico Nardelli. Do we really need computational thinking? Communications of the ACM, 62(2):32–35, January 2019. doi:10.1145/3231587.
Seymour Papert. Mindstorms: children, computers, and powerful ideas. Basic Books, New York, 1980. ISBN 978-0-465-04627-0. URL: https://worrydream.com/refs/Papert_1980_-_Mindstorms,_1st_ed.pdf.
Johannes Preiser-Kapeller. Calculating the Middle Ages? The Project »Complexities and Networks in the Medieval Mediterranean and Near East« (COMMED). Medieval Worlds, medieval worlds(Volume 2015.2):100–127, 2015. doi:10.1553/medievalworlds_no2_2015s100.
Denis Roegel. The great logarithmic and trigonometric tables of the French Cadastre: a preliminary investigation. Research Report, Laboratoire lorrain de Recherche en Informatique et ses Applications, December 2010. URL: https://hal.inria.fr/inria-00543946.
Jeannette M Wing. Computational thinking and thinking about computing. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366(1881):3717–3725, October 2008. URL: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2696102/ (visited on 2022-05-30), doi:10.1098/rsta.2008.0118.
