Part 1: Exercises#
Exercise 1
What are all the possible sentences that one can produce using the regular grammar introduced in Section “Historic hero: Noam Chomsky”?
Solution to Exercise 1
I write
you write
I read
you read
Exercise 2
What is the result of applying the second natural language definition of the Fibonacci function in Section “Natural languages vs programming languages” using “7” as input?
Solution to Exercise 2
13
Exercise 3
Write down two objects or situations that refer to the same pattern if analysed from an abstract point of view, as introduced in Section “Abstraction is the key”. What features do they have in common?
Solution to Exercise 3
Situations:
Creating a specific color hue of acrylic paint
Making bechamel
Common features:
Different ingredients have to be mixed in together
There is a specific result desired, in terms of color and consistency
For the result to be achieved, each ingredient has to be added in specific amounts
Constant stirring is necessary, and at a specific speed
Sense of touch, vision, and smell are engaged
Note
Answer provided by Delfina Pandiani in 2018.
Exercise 4
What is the result of the execution of the algorithm in Figure 9 of the chapter “Algorithms” using "Peroni", "HTML", and "Peroni, S., Osborne, F., Di Iorio, A., Nuzzolese, A. G., Poggi, F., Vitali, F., Motta, E. (2017). Research Articles in Simplified HTML: a Web-first format for HTML-based scholarly articles. PeerJ Computer Science 3: e132. e2513. DOI: https://doi.org/10.7717/peerj-cs.132" as input values?
Solution to Exercise 4
2
Exercise 5
Write the flowchart of an algorithm that takes in input two objects and returns the string “yes” whether the two objects are the same; otherwise, it returns the string “no”.
Solution to Exercise 5
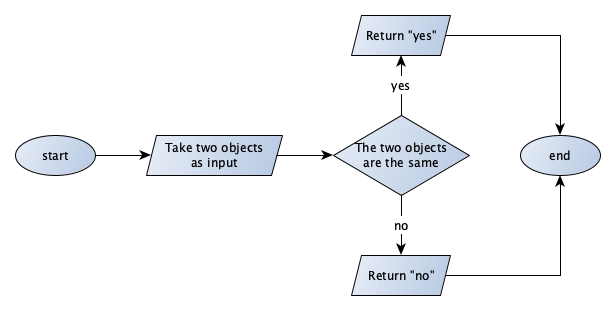
The source GraphML file (that can be open and modified with yEd) of the flowchart is available as part of the material of the course.
Exercise 6
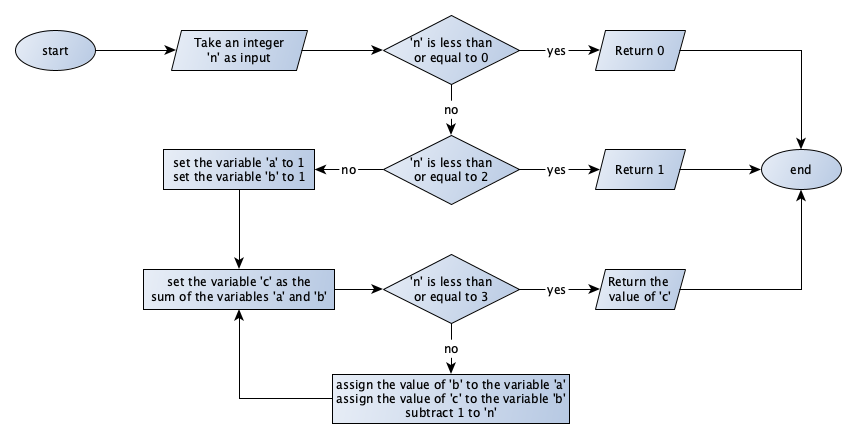
The Chapter “Introduction to Computational Thinking” illustrates two different algorithms expressed in natural language, for implementing the Fibonacci function. Create two distinct flowcharts to implement both of them.
Solution to Exercise 6
Flowchart for Fibonacci, definition 1:
Flowchart for Fibonacci, definition 2:
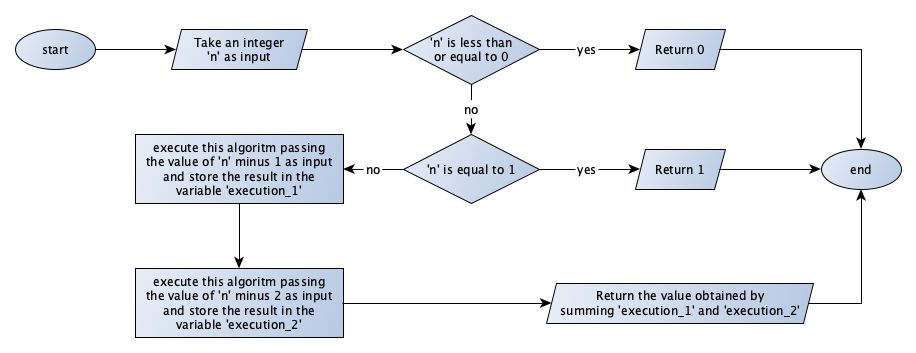
The source GraphML file (that can be open and modified with yEd) of the flowcharts of the two exercises are available as part of the material of the course (first flowchart, second flowchart).
Exercise 7
Write the table of instructions of a Turing machine with four states – A (initial state), B, C, and D (final state) – such that, once the final state is reached, only the cells immediately on the left and on the right of the initial position of the head of the machine will have the value 1 specified. The final state must not have any instruction set in the table.
Solution to Exercise 7
The table of instructions of the Turing machine is as follows:
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
| A | 0 | 1 | right | B |
| A | 1 | 0 | left | C |
| B | 0 | 1 | left | A |
| C | 0 | 1 | left | D |
The starting state is A while the ending state is D.
The same machine, specified in the format used in the Turing machine visualisation website, is available as follows.
blank: '0'
start state: A
table:
A:
0: { write: 1, R: B }
1: { write: 0, L: C }
B:
0: { write: 1, L: A }
C:
0: { write: 1, L: D }
D:
The source YAML file of the Turing machine is available as part of the material of the course.
Exercise 8
Consider an algorithm that takes as input a 0-1 sequence of exactly five symbols and returns 1 if the sequence contains at least three consecutive 1s, and returns 0 otherwise. Implement the algorithm using a Turing machine, with the cell corresponding to the head’s starting position storing the final result. Also, the five cells following the starting position of the head are initialised with the 0-1 sequence of five symbols used as input to the algorithm.
Solution to Exercise 8
The table of instructions of the Turing machine is as follows:
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
| start | 0 | 1 | right | pn |
| pn | 0 | 0 | right | p0 |
| pn | 1 | 0 | right | p1 |
| p0 | 0 | 0 | right | p00 |
| p0 | 1 | 0 | right | p01 |
| p1 | 0 | 0 | right | p00 |
| p1 | 1 | 0 | right | p11 |
| p00 | 0 | 0 | left | fail |
| p00 | 1 | 0 | right | p001 |
| p01 | 0 | 0 | left | fail |
| p01 | 1 | 0 | right | p011 |
| p11 | 0 | 0 | left | fail |
| p11 | 1 | 0 | left | stop |
| p001 | 0 | 0 | left | fail |
| p001 | 1 | 0 | right | p0011 |
| p011 | 0 | 0 | left | fail |
| p011 | 1 | 0 | left | stop |
| p0011 | 0 | 0 | left | fail |
| p0011 | 1 | 0 | left | stop |
| fail | 0 | 0 | left | fail |
| fail | 1 | 0 | left | stop |
The starting state is start while the ending state is stop.
The same machine, specified in the format used in the Turing machine visualisation website, is available as follows.
input: '010111'
blank: '0'
start state: start
table:
start:
0: { write: 1, R: pn }
pn:
0: { write: 0, R: p0 }
1: { write: 0, R: p1 }
p0:
0: { write: 0, R: p00 }
1: { write: 0, R: p01 }
p1:
0: { write: 0, R: p00 }
1: { write: 0, R: p11 }
p00:
0: { write: 0, L: fail }
1: { write: 0, R: p001 }
p01:
0: { write: 0, L: fail }
1: { write: 0, R: p011 }
p11:
0: { write: 0, L: fail }
1: { write: 0, L: stop }
p001:
0: { write: 0, L: fail }
1: { write: 0, R: p0011 }
p011:
0: { write: 0, L: fail }
1: { write: 0, L: stop }
p0011:
0: { write: 0, L: fail }
1: { write: 0, L: stop }
fail:
0: { write: 0, L: fail }
1: { write: 0, L: stop }
stop:
The source YAML file of the Turing machine is available as part of the material of the course.
Exercise 9
Consider an algorithm that takes as input a 0-1 sequence of exactly five symbols and returns 1 if the sequence contains at least three 1s in any order, while it returns 0 otherwise. Implement the algorithm using a Turing machine, with the cell corresponding to the head’s starting position storing the final result. Also, the five cells following the starting position of the head are initialised with the 0-1 sequence of five symbols used as input to the algorithm.
Solution to Exercise 9
The table of instructions of the Turing machine is as follows:
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
| start | 0 | 1 | right | pn |
| pn | 0 | 0 | right | p0 |
| pn | 1 | 0 | right | p1 |
| p0 | 0 | 0 | right | p00 |
| p0 | 1 | 0 | right | p01 |
| p1 | 0 | 0 | right | p01 |
| p1 | 1 | 0 | right | p11 |
| p00 | 0 | 0 | left | fail |
| p00 | 1 | 0 | right | p001 |
| p01 | 0 | 0 | right | p001 |
| p01 | 1 | 0 | right | p011 |
| p11 | 0 | 0 | right | p011 |
| p11 | 1 | 0 | left | stop |
| p001 | 0 | 0 | left | fail |
| p001 | 1 | 0 | right | p0011 |
| p011 | 0 | 0 | right | p0011 |
| p011 | 1 | 0 | left | stop |
| p0011 | 0 | 0 | left | fail |
| p0011 | 1 | 0 | left | stop |
| fail | 0 | 0 | left | fail |
| fail | 1 | 0 | left | stop |
The starting state is start while the ending state is stop.
The same machine, specified in the format used in the Turing machine visualisation website, is available as follows.
input: '010001'
blank: '0'
start state: start
table:
start:
0: { write: 1, R: pn }
pn:
0: { write: 0, R: p0 }
1: { write: 0, R: p1 }
p0:
0: { write: 0, R: p00 }
1: { write: 0, R: p01 }
p1:
0: { write: 0, R: p01 }
1: { write: 0, R: p11 }
p00:
0: { write: 0, L: fail }
1: { write: 0, R: p001 }
p01:
0: { write: 0, R: p001 }
1: { write: 0, R: p011 }
p11:
0: { write: 0, R: p011 }
1: { write: 0, L: stop }
p001:
0: { write: 0, L: fail }
1: { write: 0, R: p0011 }
p011:
0: { write: 0, R: p0011 }
1: { write: 0, L: stop }
p0011:
0: { write: 0, L: fail }
1: { write: 0, L: stop }
fail:
0: { write: 0, L: fail }
1: { write: 0, L: stop }
stop:
The source YAML file of the Turing machine is available as part of the material of the course.
