Organising information: graphs#
This chapter introduces the last data structure presented in this course, i.e. the graph. The historic hero introduced in these notes is Leonhard Euler, a great scientist of the 18th century who introduced a new mathematical field called graph theory for the very first time.
Note
The slides for this chapter are available within the book content.
Historic hero: Euler#
Leonhard Euler (shown in Fig. 50) was one of the most influential men of Science of whole history. His contributions in Mathematics, Physics, Astronomy, Logic, among others, were disruptive and even started pretty new disciplines. He spent most of his life in Saint Petersburg in Russia. Among the mathematical problems he dealt with, one related to a hilarious story that he solved by initiating a new field in mathematics called graph theory.
The (mathematical) story told about the seven bridges of the city of Königsberg, illustrated in Fig. 51. We can state the problem as follows: is it possible to walk around the town and cross each bridge once and only once? Several people have tried to propose a solution to this enigma before Euler. Finally, he demonstrated it through purely mathematical (and non-debatable) proof [Eul41].

Fig. 50 A portrait of Leonard Euler by Emanuel Handmann. Picture by Oursana, source: Wikipedia.#
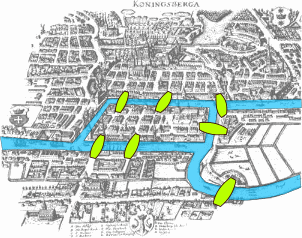
Fig. 51 A representation of the seven bridges in Königsberg. Figure by Bogdan Giuşcă, source: Wikimedia Commons.#
He abstractly described the four lands in Königsberg divided by the river as nodes of a network, where each edge between two nodes represents one of the city’s bridges. Figure 3 shows his abstract representation of the problem. Using this abstract notion, known as graph, he demonstrated that there is no solution to the problem of the seven bridges of Königsberg.
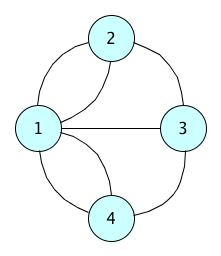
Fig. 52 An abstract representation of the seven bridges of Königsberg using a graph.#
He based the solution to the problem on the following intuition. The idea was that each node, excepting the starting node and the final node, should have an even number of edges. It is a practical implication: one should pass through two different bridges (i.e. arts) to enter and then go out from a node. Thus, non-starting and non-ending nodes must have an even number of edges for being satisfactorily traversed one or more times. However, all the nodes in Fig. 52 have an odd number of edges, which contradicts the aforementioned requirement.
Graphs#
Graphs are one of the principal data structures in Computer Science and Computational Thinking. For example, they describe routes between cities, connections to people in social networks, the organisation of links between Web pages, etc. [AB02]. Graphs are entirely derived from the mathematical structure invented by Euler, as illustrated in Section Historic hero: Euler. In particular, we can distinguish two different kinds of graphs: undirected graphs and directed graphs. In undirected graphs, used by Euler in the seven bridges problem, one can traverse an edge in one way or the other indifferently. Instead, the edge specifies the direction for crossing it in directed graphs.
In Python, as it happens for the trees, there is no built-in class defining this type of object. However, several external libraries implement them. Among the most used and famous there is NetworkX. This library makes available the common constructs for creating and traversing graphs and additional functions for analysing them for different purposes, such as for the analysis of social networks.
Undirected graphs#
We can create an undirected graph using the constructor Graph(). Then, we make all the nodes and edges of such a new graph by using its available methods.
as part of the material of the course.# 1from networkx import Graph
2
3# create a new graph
4my_graph = Graph()
5
6# create four nodes
7my_graph.add_node(1)
8my_graph.add_node(2)
9my_graph.add_node(3)
10my_graph.add_node(4)
11
12# create five edges
13my_graph.add_edge(1, 2)
14my_graph.add_edge(1, 3)
15my_graph.add_edge(1, 4)
16my_graph.add_edge(2, 3)
17my_graph.add_edge(3, 4)
The NetworkX package allows us to associate an immutable object as a node. We can connect such a node through one or more edges. In particular, it is possible to execute the following methods on a graph object:
<graph>.add_node(<node>)adds<node>as a node of the graph – note that, if a node with that value is already present, the method does not affect the graph;
<graph>.add_edge(<node_1>, <node_2>)adds an edge between<node_1>and<node_2>– note that, since we are dealing with undirected graphs, inverting the position of the input nodes does not change the result;
<graph>.remove_node(<node>)removes<node>from the graph as well as all the edges that involve it directly;<graph>.remove_edge(<node_1>, <node_2>)removes the particular edge between the two nodes specified.
Listing 58 introduces an example of a graph. It creates a structure similar to the one presented in Fig. 52, except it is impossible to make multiple arcs between two nodes. Thus, using this specific constructor, it is impossible to create the same structure requested by Euler for solving the mathematical problem introduced in Section Historic hero: Euler.
as part of the material of the course.# 1from networkx import MultiGraph
2
3# create a new graph
4my_graph = MultiGraph()
5
6# create four nodes
7my_graph.add_node(1)
8my_graph.add_node(2)
9my_graph.add_node(3)
10my_graph.add_node(4)
11
12# create seven edges
13my_graph.add_edge(1, 2)
14my_graph.add_edge(1, 2)
15my_graph.add_edge(1, 3)
16my_graph.add_edge(1, 4)
17my_graph.add_edge(1, 4)
18my_graph.add_edge(2, 3)
19my_graph.add_edge(3, 4)
To enable the creation of multiple edges between two nodes, we have to use a different kind of undirected graph using the constructor MultiGraph(). This graph accepts multiple edges between nodes by calling the method <graph>.add_edge(<node_1>, <node_2>) several times, and the method <graph>.remove_node(<node>) will remove all the edges involving that input node, as usual. Listing 59 introduces an example of this kind of graph that maps precisely the one introduced in Fig. 52.
Two additional methods are fundamental to understanding how a graph is composed and which nodes link to the others. They are <graph>.nodes() and <graph>.edges(), each returning a particular kind of lists (called NodeView and EdgeView respectively) that can be iterated by means of a for-each loop as usual. It is also possible to understand what are the nodes linked by a target node using the adjacency variable <graph>.adj[<node>]. This operation returns an AtlasView: a kind of dictionary containing all the nodes reachable from <node>, where each dictionary key represents one of these nodes.
as part of the material of the course.# 1from networkx import Graph
2
3# create a new graph
4my_graph = Graph() # it works also with MultiGraph
5
6my_graph.add_node(1) # no additional data
7my_graph.add_node(2, name="John", surname="Doe") # additional data
8my_graph.add_node(3)
9
10my_graph.nodes()
11# Returns NodeView (tuple) with all the nodes:
12# NodeView((1, 2, 3))
13
14my_graph.nodes(data=True)
15# Returns a NodeDataView (like a dictionary) with nodes + data:
16# NodeDataView({1: {}, 2: {'name': 'John', 'surname': 'Doe'}, 3: {}})
17
18my_graph.add_edge(1, 2) # no additional data
19my_graph.add_edge(1, 3, weight=4) # additional data
20
21my_graph.edges()
22# Returns an EdgeView (of two-item tuples) with all the edges:
23# EdgeView([(1, 2), (1, 3)])
24
25my_graph.edges(data=True)
26# Returns an EdgeDataView (of three-item tuples) with edges + data:
27# EdgeDataView([(1, 2, {}), (1, 3, {'weight': 4})])
28
29my_graph.adj[1]
30# This returns an AtlasView (like a dictionary) containing all the
31# nodes that are reachable from an input one + data of edges:
32# AtlasView({2: {}, 3: {'weight': 4}})
The value associated with each node, in this case, is another dictionary that is initialised empty if one did not specify any additional information explicitly. This information, or attribute in NetworkX, can be specified when one builds the edge connecting the two nodes. In particular, we use one or more pairs of a parameter and the value assigned to him via =, as shown in Listing 60. We can do the same kind of assignments to nodes. In addition, these information can be also shown by executing the aforementioned methods nodes() and edges() by specifying the named parameter data as True, i.e. <graph>.nodes(data=True) and <graph>.edges(data=True). This use of naming the parameters explicitly in Python when one wants to execute a method (or a function) is permissible by Python, as explained in its documentation.
Directed graphs#
According to the NetworkX package, we can create a directed graph with the constructor DiGraph(). In NetworkX, a direct graph has the same methods of undirected graphs, presented in Section Historic hero: Euler. However, in this case, the order between <node_1> and <node_2> in the methods for adding and removing an edge is meaningful, since an edge specifies a particular direction: <node_1> is the source node, while <node_2> is the target node.
Also, it is possible to specify more than one edge between two nodes by using the constructor MultiDiGraph(). For instance, Fig. 53 shows the abstract diagram of the graph implemented in Listing 59 if the constructor MultiDiGraph() would be used instead of MultiGraph().
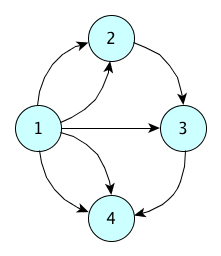
Fig. 53 The diagram of the graph depicted in Fig. 52 and implemented in Listing 58 if we use MultiDiGraph() instead of MultiGraph().#
References#
Réka Albert and Albert-László Barabási. Statistical mechanics of complex networks. Reviews of Modern Physics, 74(1):47–97, January 2002. URL: https://arxiv.org/pdf/cond-mat/0106096.pdf (visited on 2025-10-11), doi:10.1103/RevModPhys.74.47.
Leonhard Euler. Solutio problematis ad geometriam situs pertinentis. In Commentarii academiae scientiarum Petropolitanae, volume 8, pages 128–140. Euler Archive, 1741. URL: http://eulerarchive.maa.org/docs/originals/E053.pdf.
